Repeat after me: “statistical significance is not everything.”
It’s just as important to have some measure of how practically significant an effect is, and this is done using what we call an effect size.
Cohen’s d is one of the most common ways we measure the size of an effect.
Here, I’ll show you how to calculate it. If you’d rather skip all that, you can download a free spreadsheet to do the dirty work for you right here. Just use this form to sign up for the spreadsheet, and for more practical updates like this one:
(We will never share your email address with anybody.)
The spreadsheet will also share a confidence interval and margin of error for your Cohen’s d.
The Formula
Cohen’s d is simply a measure of the distance between two means, measured in standard deviations. The formula used to calculate the Cohen’s d looks like this:
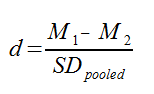
Where M1and M2 are the means for the 1st and 2nd samples, and SDpooled is the pooled standard deviation for the samples. SDpooled is properly calculated using this formula:
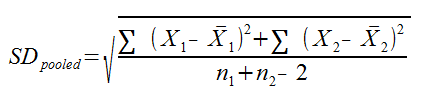
In practice, though, you don’t necessarily have all this raw data, and you can typically use this much simpler formula:
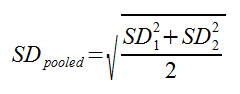
The spreadsheet I’ve included on this page allows you to use either formula.
In the first, more lengthy formula, X1 represents a sample point from your first sample, and Xbar1 represents the sample mean for the first sample. The distance between the sample mean and the sample point is squared before it is summed over every sample point (otherwise you would just get zero). Obviously, X2 and Xbar2 represent the sample point and sample mean from the second sample. n1 and n2 represent the sample sizes for the 1st and 2nd sample, respectively.
In the second, simpler formula, SD1 and SD2 represent the standard deviations for samples 1 and 2, respectively.
Now for a few frequently asked questions.
Can your Cohen’s d have a negative effect size?
Yes, but it’s important to understand why, and what it means. The sign of your Cohen’s d depends on which sample means you label 1 and 2. If M1 is bigger than M2, your effect size will be positive. If the second mean is larger, your effect size will be negative.
In short, the sign of your Cohen’s d effect tells you the direction of the effect. If M1 is your experimental group, and M2 is your control group, then a negative effect size indicates the effect decreases your mean, and a positive effect size indicates that the effect increases your mean.
How is Cohen’s d related to statistical significance?
It isn’t.
It’s important to understand this distinction.
To say that a result is statistically significant is to say that you are confident, to 100 minus alpha percent, that an effect exists. Statistical significance is about how sure you are that an effect is real; it says nothing about the size of the effect.
By contrast, Cohen’s d and other measures of effect size are just that, ways to measure how big the effect is (and in which direction). Cohen’s d tells you how big the effect is compared to the standard deviation of your samples. It says nothing about the statistical significance of the effect. A large Cohen’s d doesn’t necessarily mean that an effect actually exists, because Cohen’s d is just your best estimate of how big the effect is, assuming it does exist.
(Of course, if you have a confidence interval for your Cohen’s d, then the confidence interval can tell you whether or not the effect is significant, depending on whether or not it contains 0.)
Can you convert between Cohen’s d and r, and if so, when?
There is a relationship between Cohen’s d and correlation (r). The following formula is most commonly used to calculate d from r:

And this formula is used to find r from d:

Where a is a correlation factor found using the sample sizes:

However, it’s important to realize that these conversions can sometimes change your interpretation of the data, in particular when base rates are important. You can find an in depth academic discussion of conversions between the two in this paper.
For conversions between d and the log odds ratio, you can also take a look at this paper.
Can you statistically compare two independent Cohen’s d results?
Yes, but not at face value, and only with extreme caution.
Remember, Cohen’s d is the difference between two means, measured in standard deviations. If two experiments are sampled from different populations, the standard deviations are going to be different, so the effect size will also be different.
For example, you can’t compare the effect size of an antidepressant on depressed people with the effect size of an antidepressant on schizophrenic people. The inherent variance of the sample populations are going to be different, so the resulting effect sizes are also going to be different.
Assuming that the experiments were both conducted on the same population, it’s still not a good idea to compare Cohen’s d results at face value. If one value is larger, this doesn’t mean there is a statistically significant difference between the two effect sizes.
The simplest way to compare effect sizes is by their confidence intervals
If the confidence intervals overlap, the difference isn’t statistically significant. To find the confidence interval, you need the variance. The variance of the Cohen’s d statistic is found using:

You can use this variance to find the confidence interval. You can also use the spreadsheet I’ve provided on this page to get the confidence interval.
Can you calculate Cohen’s d from the results of t-tests or F-tests?
Yes, you can. This paper explains how to do that beautifully. If there’s enough demand for it, I might put together a spreadsheet for this also.
Want to download the Cohen’s d spreadsheet and let it do the dirty work? Sign up here: